5-cell honeycomb
| 4-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform honeycomb |
| Family | Simplectic honeycomb |
| Schläfli symbol | {3[5]} |
| Coxeter–Dynkin diagrams | |
| 4-face types | {3,3,3} t1{3,3,3} |
| Cell types | {3,3} t1{3,3} |
| Face types | {3} |
| Vertex figure | t0,3{3,3,3} |
| Coxeter groups | 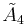 , [3[5]] , [3[5]] |
| Properties | vertex-transitive |
In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb. It is composed of 5-cells (pentachora) and rectified 5-cells (dispentachora) facets in a ratio of 1:1.
Cells of the vertex figure are ten tetrahedrons and 20 triangular prisms, corresponding to the ten 5-cells and 20 rectified 5-cells that meet at each vertex. All the vertices lie in parallel realms in which they form alternated cubic honeycombs, the tetrahedra being either tops of the dispentachora or the bases of the pentachora, and the octahedra being the bottoms of the dispentachora.[1]
This vertex arrangement is called the A4 lattice, or 4-simplex lattice. The 20 vertices of its vertex figure, the runcinated 5-cell represent the 20 roots of the 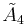 Coxeter group.[2]
Coxeter group.[2]
Contents |
Alternate names
- Cyclopentachoric tetracomb
- Pentachoric-dispentachoric tetracomb
Related polytopes and honeycombs
The tops of the 5-cells in this honeycomb adjoin the bases of the 5-cells, and vice versa, in adjacent laminae; but alternating laminae may be inverted so that the tops of the rectified 5-cells adjoin the tops of the rectified 5-cells and the bases of the 5-cells adjoin the bases of other 5-cells. This inversion results in another non-Wythoffian uniform convex honeycomb. Octahedral prisms and tetrahedral prisms may be inserted in between alternated laminae as well, resulting in two more non-Wythoffian elongated uniform honeycombs.[3]
This honeycomb is one of 7 unique uniform honycombs[4] constructed by the 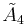 Coxeter group. The other 6 have Coxeter–Dynkin diagrams as: , , , ,, .
Coxeter group. The other 6 have Coxeter–Dynkin diagrams as: , , , ,, .
See also
- Regular and uniform honeycombs in 4-space:
Notes
References
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs) Model 134
- Richard Klitzing, 4D, Euclidean tesselations, x3o3o3o3o3*a - cypit - O134